Example 1: x2 + 5x + 2 = 0
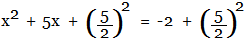
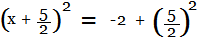

The square root on the LHS cancels out the exponent of 2,
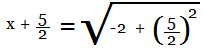
Simplifyt he RHS,
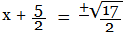
The square root of a number can be positive or negative, so put a 'plus below minus' sign before the RHS, and move fraction 5/2 to RHS,
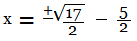
Solve further,

Solution:
Steps 1, 2 and 3:
The given equation is already in the standard form, so there is no need to convert it to the standard form. Further, the coefficient of x-squared is 1, so on dividing the equation by it the equation will remain unchanged; So there is no need to divide the equation by the coefficient of x-squared. Move the constant term to RHS,
x2 + 5x = -2
Step 4:
- Take the coefficient of 'x': 5
- Divide it by 2: 5/2
- Square it: (5/2)2
- Add it to both sides of the equation:
Step 5:
Comparing the LHS with a2 + 2ab + b2, we obtain 'a' = x and 'b' = (5/2). Now since the LHS is in the form of a2 + 2ab + b2, therefore it can be rewritten as (a + b)2, because of the mathematical property (a + b)2 = a2 + 2ab + b2. Thus,
Step 6:
Now that x-squared has been completely factored from the equation, it can be solved for 'x'. Take square roots of both sides in order to remove the square on LHS, The square root on the LHS cancels out the exponent of 2,
Simplifyt he RHS,
The square root of a number can be positive or negative, so put a 'plus below minus' sign before the RHS, and move fraction 5/2 to RHS,
Solve further,
Answer: 
Example 2: 2x2 + 4x = -2
Solution:
Step 1: Convert to Standard Form

Step 2: Divide by coefficient of x-squared:
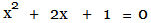
Step 3: Move constant term to RHS:

Step 4: Take coefficient of 'x', divide it by 2, then square it. Add the result to LHS and RHS,

Step 5: Compare the LHS with a2 + 2ab + b2 and apply the formula (a + b)2 = a2 + 2ab + b2
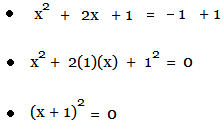
Step 6: Solve for 'x':

Step 2: Divide by coefficient of x-squared:
Step 3: Move constant term to RHS:
Step 4: Take coefficient of 'x', divide it by 2, then square it. Add the result to LHS and RHS,
Step 5: Compare the LHS with a2 + 2ab + b2 and apply the formula (a + b)2 = a2 + 2ab + b2
Step 6: Solve for 'x':
Answer: x = -1
Example 3: 6p2 = -11p - 10
Solution:
Step 1: Convert to Standard Form
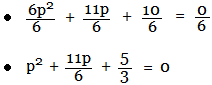
Step 3: Move constant term to RHS:
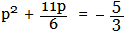
Step 4: Take coefficient of 'p', divide it by 2, then square it. Add the result to LHS and RHS,

Step 5: Compare the LHS with a2 + 2ab + b2 and apply the formula (a + b)2 = a2 + 2ab + b2

Step 6: Solve for 'p' (by taking square roots on both sides):

6p2 + 11p + 10 = 0
Step 2: Divide by coefficient of p-squared: Step 3: Move constant term to RHS:
Step 4: Take coefficient of 'p', divide it by 2, then square it. Add the result to LHS and RHS,
Step 5: Compare the LHS with a2 + 2ab + b2 and apply the formula (a + b)2 = a2 + 2ab + b2
Step 6: Solve for 'p' (by taking square roots on both sides):
Answer: 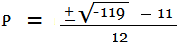

No comments:
Post a Comment