| General steps for completing the square |
are written in the standard form. This method uses the algebraic property of expansion
of the square of the sum of two terms, which means:
In this method, simple mathematical operations are applied to a Quadratic Equation
(written in the standard form) in order to make its LHS (Left Hand Side) expression
of the form a2 + 2ab + b2. Then the LHS expression is factored
to the form (a + b)2 by applying the above mentioned property. The following
example will further clarify this method:
Equation:
2x2 + 5x + 3
Solution:
by the coefficient of x-squared.
The coefficient of x-squared is 2, so dividing the equation throughout by 2,


term to the RHS (Right Hand Side).
The constant term is 3/2, so moving it to RHS,

'x', divide it by 2, then square it. Add the resulting term to both sides of the
equation (That is, add it to LHS as well as RHS).
Coefficient of 'x' is 5/2. Dividing it by 2, we obtain 5/4. Squaring it, we obtain
25/16. Adding 25/16 to both sides,

Simplifying the RHS,

25/16. Adding 25/16 to both sides,
Simplifying the RHS,
+ 2ab + b2 and factor it to (a + b)2.
The LHS is now in the form of a2 + 2ab + b2, where 'a' is
'x' and 'b' is 5/2. Applying the property a2 + 2ab + b2 =
(a + b)2, the LHS is written in the form (a + b)2,
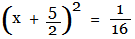
'x' and 'b' is 5/2. Applying the property a2 + 2ab + b2 =
(a + b)2, the LHS is written in the form (a + b)2,
Taking square root of both LHS and RHS,


Move '5/2' to RHS,

Either
Move '5/2' to RHS,
Either
or
- Divide the equation throughout by coefficient of x-squared
- Move the constant term to RHS
- Take the coefficient of 'x', divide it by 2, square it, and then add it to LHS and RHS of the equation
- Compare the LHS with a2 + 2ab + b2 and write it in the form of (a + b)2
- Solve for 'x' by taking square root on both sides.
No comments:
Post a Comment