Transformations of functions

Functions can produce graphs on the coordinate plane. The graph of a function can be moved up, down, left or right, and can be stretched or compressed vertically as well as horizontally by adding, subtracting, multiplying or dividing values to its function in a special way. 

Function transformations discuss the effect of adding, subtracting, multiplying or dividing quantities from/to a function on its graph.

Vertical shift example

Vertical translation/shift

Add/subtract a number to the function to move it up and down.

• Move up: `f(x)+ D`
• Move down: `f(x) – D`

Example

`f(x)= x^2`

• Move up 2 units: `f(x)+ 2 = x^2+ 2`
• Move down 2 units: `f(x) - 2 =x^2 - 2`

Horizontal translation/shift

Horizontal shift example

Add/subtract a number to the variable ‘x’

• Move right `f(x – C)`
• Move left `f(x + C)`

Example

`f(x)= x^2`

• Move right 10 units `f(x -3)=(x-3)^2`
• Move left 10 units `f(x +3)=(x+3)^2`

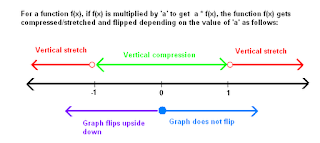
Vertical stretch/compression

Vertical strech/compression diagrammatic explanation

Multiply a value to the whole function: `a*f(x)`. This transformation does two things to graph:

Vertical stretch/compression

• Compress: `a < 1` or if `-1 < a < 1`
• Stretch : `a > 1` or `a < -1 or a > 1`

Upside down flips (reflection in the x-axis):

• Flips upside down if `a < 0`
• Does not flip if `a > 0`

Special cases:

• `a = 0` then you have compressed the function into the x-axis because `0 * f(x)= 0`
• `a = 1` then you have not changed the function at all because `1 * f(x)= f(x)`
• `a = -1` does not vertically stretch or compress, just flips it upside down or reflects it in the x-axis

Examples

`f(x) = x^2 + 2x`

• Vertical stretch by a factor of 4: `4*f(x)=4(x^2+2x)`

• Vertically compress by a factor of 4: `1/4*f(x)=1/4 (x^2+2x)`

• Vertically stretch by a factor of 4 and flip upside down: `-4*f(x)= -4(x^2+2x)`

• Vertically compress by a factor of 4 and flip upside down: `-1/4*f(x)=-1/4 (x^2+2x)`

Horizontal stretch/compression

Multiply the function’s variable with a number. That is `f(b*x)`. This transformation does two things to a graph:

Horizontal stretch/compress:

• Horizontal compression: `b > 1` or b `< -1 or b> 1`
• Horizontal stretch: `b < 1` or `-1 < b < 1`

Flip right to left (or reflection in y-axis):

• `b < 0` then the graph flips left to right or gets reflected in the y-axis
• `b > 0`, then the graph does not flip at all

Special cases:

• `b=0`, the function gets compressed to a horizontal line
• `b=1`, the function will remain same as `f(1*x) = f(x)`
• `b=-1`, the function will get flipped left to right or reflected in the y-axis and it does not get horizontally stretched or compressed

Examples

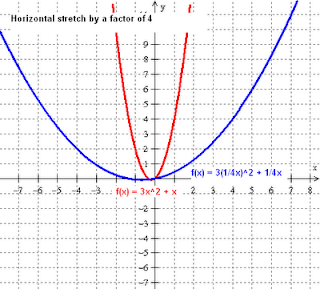
`f(x)= 3x^2+ x`

• Horizontal compression by a factor of 4: `f(4x)= 3(4x)^2+ 4x`

• Horizontal stretch by a factor of 4: `f(1/4 x)= 3(1/4 x)^2+1/4 x`

• Horizontal compression by a factor of 4 with reflection in y-axis (left to right flip)

• Horizontal stretch by a factor of 4 with reflection in y-axis (left to right flip)

More than one transformations

You can apply one or more transformations to a function. In fact, you can apply all of the above transformations to a function, but in a specific order. Notice that in the above transformations

• The letter ‘a’ is assigned for vertical stretch/compression,
• ‘b’ is assigned for horizontal stretch/compression,
• ‘c’ is assigned for horizontal translation/shift, and
• ‘d’ is assigned for vertical shift.

Since you say ‘ABCD’ in that order, so the transformations are applied to a function in that order as well. So if you are applying two transformations to a function, for example, vertical shift and horizontal compression, horizontal compression is done before vertical shift.

For example, if you shift a function f(x) 3 units up and vertically stretch it by a factor of 5 units, then the resulting function is `5f(x) – 3`, not `5(f(x) – 3)`, because vertical stretch/compression is applied before vertical shift, as A comes before D.