A quadratic equation can be written in its vertex form. The vertex form of a quadratic equation makes it very easy to get the coordinates of the vertex of the parabola formed by that equation. It is thus very easy to graph a quadratic equation when it is given in the vertex form.
The vertex form of a quadratic equation is as follows:
y = a(x - h)^2 + kVertex of the above quadratic equation is given by (h, k)
A number of different features of the parabola can be determined from a quadratic equation written in the vertex form:
- If 'a' in the above equation is a positive number, then the parabola of the equation is shaped like a 'U'.
- If 'a' in the above equation is a negative number, then the parabola of the equation is shaped like an upside down 'U'.
- If the value of 'a' in the above equation increases more than 1, then the graph of its equation becomes narrower.
- If the value of 'a' in the above equation decreases from 1, then the graph of its equation becomes wider.
- If the value of 'a' in the above equation is zero, then it becomes a straight line lying on the x axis. (it is neither a parabola nor a quadratic equation if a = 0)
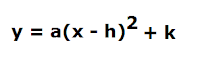

Here is what I think about vertex as in a graphical wave form, a parabola which opens up has a lowest point and a parabola which opens down has a highest point and the highest or lowest point on a parabola is called the vertex.
ReplyDelete