| Go to the Main article on Quadratic Equations. There are two ways to learn the method of completing the square in order to solve a quadratic equation. One is to learn it visually, in which you consider a quadratic equation as an incomplete square, and, in order to complete that square, you rewrite the quadratic equation appropriatele. The other method is to learn a few steps, and apply them to any quadratic equation that you want to solve with the method of completing the square. We will learn both methods, and let us start with the first one first. The method of completing the square: Understanding it Visually |
Take an example of the quadratic equation
x^2 + 6x + 5 = 0Now to view it as an incomplete square, we are going to follow these steps:
- Step 1: Take on the 'x^2' and 'x' terms from the quadratic equation: x^2 + 6x
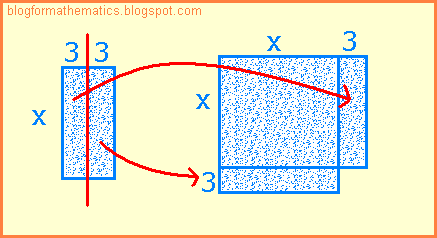
- Step 2: Represent them as a square and a rectangle:
- Step 3: Try to split the rectangle into two parts, and put each part on one side of the square. This will make an incomplete bigger square.
 |
| Represents x^2 + 6x |
Caption: So this (the above figure) represents x^2 + 6x as an incomplete square. For now, we will be ignoring the number part (which is 5).
- Step 4: Now we need to add a 3 x 3 square to the above incomplete square in order to make it a complete square. But from where will we get it? We can't just plug in a square because we want to. So this means that if we add the 3 x 3 square to the above figure, we will also need to subtract it like this:
Caption: Now we can write the above two squares as an expression, like this:
(x + 3)^2 - 3^3Now add the 5 which we had left in the above procedure, so we get
(x + 3)^2 - 3^3 + 5
= (x + 3)^2 - 9 + 5
= (x + 3)^2 - 4Therefore we can now write the quadratic equation as:
(x + 3)^2 - 4 = 0You must notice that the single x^2 term has "vanished", and this means that we have "completed the square". Now, solving the quadratic equation, we get:
(x + 3)^2 - 4 = 0Moving 4 to the other side,
(x + 3)^2 = 4Taking square roots on both sides,
sqrt[ (x + 3)^2 ] = +/- sqrt[ 4 ]
x + 3 = (+/-)2Moving 3 to the other side,
x = (+/-)2 - 3Either x = 2 - 3 or x = -2 - 3
Either x = -1 or x = -5
The method of completing the square: Step by step
The following steps apply, in general, to all quadratic equations that can be factored by the method of completing the square. There are some quadratic equations, that do not get factored easily because they require the help of irrational numbers. We are dealing with only the rational number quadratic equations, and the following steps will help you solve such quadratic equations easily by the method of completing the square:
We will study the steps with the help of an example,
2x^2 + 12x + 10 = 0Step 1: Move the number 10 to the other side.
2x^2 + 12x = -10Step 2: Divide the whole equation by the coefficient of x^2.
x^2 + 6x = -5Step 3: Take the coefficient of 'x', divide it by 2, square it, and then add this to both sides of the equation.
- Coefficient of 'x' = 6
- Divide by 2 = 3
- Square it = 3^2
x^2 + 6x + 3^2 = -5 + 3^2Step 4: Now rewrite the left hand side as a square expression like this:
(x + 3)^2 = -5 + 9
(x + 3)^2 = 4Step 5: Take the square root on both sides.
sqrt[ (x + 3)^2 ] = sqrt[ 4 ]
x + 3 = (+/-) 2Either x + 3 = 2 or x + 3 = -2
Either x = -1 or x = -5
Therefore we solved the quadratic equation with the help of the method of completing the square. The above mentioned steps also apply to other quadratic equations.

No comments:
Post a Comment