If the quadratic is given in the vertex form, it is very easy to find out the coordinates of the vertex form the equation/function.
As a rule, for the quadratic in the vertex form `y = a(x - h)^2 + k` the coordinates of the vertex are given by `(h, k)`
For example, for the quadratic function:
After obtaining the coordinates of the vertex from the given quadratic equation/function, we need to get the x-intercepts of the parabola. In order to obtain the x-intercepts of the quadratic, solve the quadratic for f(x) = 0, that is, we will solve the equation:
Now plot the vertex and the x-intercepts of the given quadratic and join them by a freehand curve in order to obtain the parabola. For the quadratic `2(x - 3)^2 - 8`, the graph is as follows:
As a rule, for the quadratic in the vertex form `y = a(x - h)^2 + k` the coordinates of the vertex are given by `(h, k)`
For example, for the quadratic function:
`f(x) = 2(x - 3)^2 - 8`the coordinates of the vertex are (3, -8)
After obtaining the coordinates of the vertex from the given quadratic equation/function, we need to get the x-intercepts of the parabola. In order to obtain the x-intercepts of the quadratic, solve the quadratic for f(x) = 0, that is, we will solve the equation:
`2(x - 3)^2 - 8 = 0`Therefore the x-intercepts of the above equation are (5, 0) and (1, 0). If x-intercepts of a parabola don't exist, or if the x-intercept coincides with the vertex, then you need to find one or more points on either side of the axis of symmetry.
`2(x - 3)^2 = 8`
`(x - 3)^2 = 4`
`x - 3 = sqrt(4)`
`x - 3 = 2 or x - 3 = -2`
`x = 5 or x = 1`
Now plot the vertex and the x-intercepts of the given quadratic and join them by a freehand curve in order to obtain the parabola. For the quadratic `2(x - 3)^2 - 8`, the graph is as follows:
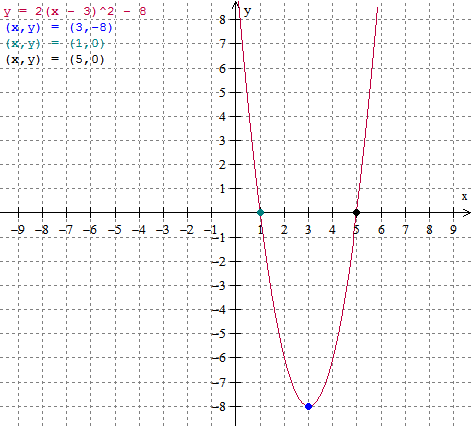 |
| Graph of `y = 2(x - 3)^2 - 8` |
No comments:
Post a Comment