There are many methods of solving a quadratic equation. The box method is especially useful in solving a quadratic equation because it helps you to factor the quadratic and thus solve it with little calculations.
In the box method, we convert a quadratic equation from a three termed expression to a four termed expression by splitting the middle term into two parts. It is another approach of splitting the middle term.
We will learn the box method of solving a quadratic equation by the help of the following example:
Jump to step: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10
Step 1: Draw four boxes and number them 1 to 4.
(Back To Top)
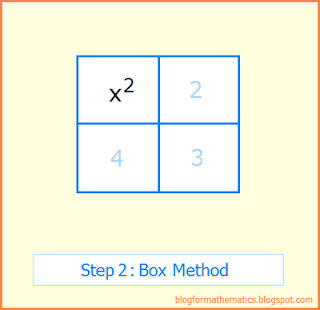
Step 2: Put the first term of quadratic in box 1.
(Back To Top)
Step 3: Put the last term of the quadratic in box 3.
(Back To Top)
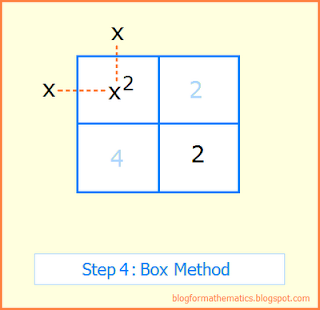
Step 4: Find two terms that multiply to give the term in box 1. Write one of these terms on the top of box 1, and the other on the left of box 1.
(Back To Top)
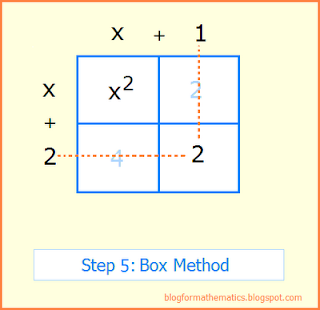
Step 5: Find two numbers that multiply to give the number in box 3. Write one of these numbers (along with its sign) over box 2, and the other on on the left of box 4.
(Back To Top)
Step 6: Multiply the term on the left of box 1 with the number on top of box 2. Write the result in box.
(Back To Top)
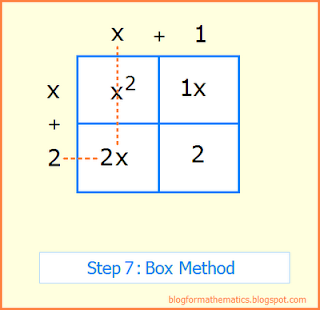
Step 7: Multiply the term on top of box 2 with the number to the left of box 4. Write the result in box 4.
(Back To Top)
Step 8: Take the term and number (along with their signs) written on the top of the four boxes and write them in a parenthesis like this:
Step 9: Take the term and number (along with their signs) written on the left of the four boxes and write them in a parenthesis as above, like this:
Step 10: Write the two parenthesis (obtained in Step 8 and Step 9) together in multiplication. This is the factored form of the original quadratic:
In order to check your answer, you can add the term in box 2 with the term in box 4. If the result equals the middle term of the original quadratic, then your solution is correct. If the two do not equate, then you need to redo the above method from Step 4. (we know that since 1x + 2x = 3x, which is the middle term of the quadratic, therefore the answer above, is correct)
Another method to check your result is to expand the two parenthesis by FOIL method. If the result equals to the original quadratic, then your solution is correct, otherwise not.
(Back To Top)
In the box method, we convert a quadratic equation from a three termed expression to a four termed expression by splitting the middle term into two parts. It is another approach of splitting the middle term.
We will learn the box method of solving a quadratic equation by the help of the following example:
x2 + 3x + 2 = 0
Jump to step: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10
Step 1: Draw four boxes and number them 1 to 4.
(Back To Top)
Step 2: Put the first term of quadratic in box 1.
(Back To Top)
Step 3: Put the last term of the quadratic in box 3.
(Back To Top)
Step 4: Find two terms that multiply to give the term in box 1. Write one of these terms on the top of box 1, and the other on the left of box 1.
(Back To Top)
Step 5: Find two numbers that multiply to give the number in box 3. Write one of these numbers (along with its sign) over box 2, and the other on on the left of box 4.
(Back To Top)
Step 6: Multiply the term on the left of box 1 with the number on top of box 2. Write the result in box.
(Back To Top)
Step 7: Multiply the term on top of box 2 with the number to the left of box 4. Write the result in box 4.
(Back To Top)
Step 8: Take the term and number (along with their signs) written on the top of the four boxes and write them in a parenthesis like this:
(x + 1)(Back To Top)
Step 9: Take the term and number (along with their signs) written on the left of the four boxes and write them in a parenthesis as above, like this:
(x + 2)(Back To Top)
Step 10: Write the two parenthesis (obtained in Step 8 and Step 9) together in multiplication. This is the factored form of the original quadratic:
(x + 1)(x + 2)(Back To Top)
In order to check your answer, you can add the term in box 2 with the term in box 4. If the result equals the middle term of the original quadratic, then your solution is correct. If the two do not equate, then you need to redo the above method from Step 4. (we know that since 1x + 2x = 3x, which is the middle term of the quadratic, therefore the answer above, is correct)
Another method to check your result is to expand the two parenthesis by FOIL method. If the result equals to the original quadratic, then your solution is correct, otherwise not.
(Back To Top)



uhm thanks :)
ReplyDeleteThis is most excellent. Thank you!
ReplyDeleteMore examples please. Thanks
ReplyDeleteThis method is Awesome!!! I was literally struggling with Splitting the middle term method. But now it became so easy because of this Box method. It could me really amazing if there were more examples provided. PLEASE PROVIDE MORE SOLVED EXAMPLES IN THIS METHOD. THANK YOU!
ReplyDeleteWhat if b=0? Then what?
ReplyDelete