Logarithmic differentiation is another way of differentiating a function. It is a way by which you simplify the process of taking the derivative of a large (and rather complex) expression, which otherwise would have been a tedious and more time consuming task.
Why and how does logarithmic differentiation simplify the process of taking derivatives of large expressions?
Logarithms were invented with the aim of simplifying large numerical calculations. This is a fact, because logarithms convert exponentiation to multiplication, multiplication to addition, and division is subtraction. For large numbers, multiplication is simpler than exponentiation, addition is simpler than multiplication, and subtraction is simpler than multiplication.
As logarithms simplify numerical calculations, they simplify differentiation of large algebraic expressions as well. And this is because they convert the power (and chain rule combined into that) into product rule, product rule into addition rule, and quotient rule to subtraction rule in context of differentiation.
The following example illustrates logarithmic differentiation:
Example: Differentiate the following function:
Differentiating the above function is a tedious task. Normally, you would differentiate this function as follows:
Differentiating without logarithms:
Apply quotient rule:
Now take the remaining derivatives in the function by using power rule and sum rule:
Apply chain rule and power rule on the remaining derivatives:
Now simplify the algebraic expression as much as possible:
If you can simplify it further, please post in comments and we will be happy to update it.
Differentiating logarithmically:
The above process can be made less tedious to do if done by the help of logarithmic differentiation. By studying the following example and the explanation provided with it, you will also learn how to do logarithmic differentiation. The method summary is provided after this example below.
Step 1: Take natural logarithm (ln) on both sides of the function:
Step 2: Apply logarithm properties to simplify right hand side further (subtraction rule and power rule for this problem)
Now take the derivative of both sides,
Step 3: Apply chain rule on left hand side:
Step 4: Differentiate the right hand side using chain rule, sum rule and power rule:
Complete the derivative on the right hand side:
We need to know f `(x), so multiply f(x) on both sides and put the original expression in place of f(x):
On simplifying the above derivative, you get the same expression as you did you when you differentiated without logarithmic differentiation.
Method of logarithmic differentiation:
- Take natural logarithm on both sides (the function name f(x) or y should be on one side of the equation)
- Completely differentiate both sides of the equation (apply chain rule on left side) - this step will give you f`(x)/f(x) on the left hand side, so for getting f`(x) (which is the derivative of f(x)) you would, at a later step, cross multiply the f(x) present below it.
- If possible, simplify the right hand side expression.
- Cross multiply f(x) from the left hand side's denominator to the right side of the equation






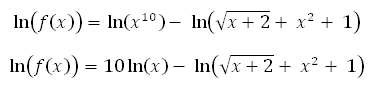





No comments:
Post a Comment