How to graph cube root functions

In order to graph cube root functions you must remember the general formula for cube root functions:

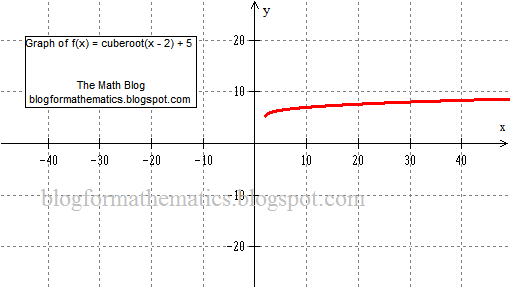
f(x) = ³√(x - h) + k

Given any cube root function, say f(x) = ³√(x - 2) + 5, compare it with the general formula to get the values of h and k. On comparing f(x) = ³√(x - 2) + 5 with the general formula, you get

• h = 2
• k = 5

Now remember that in the above general formula, h is the horizontal translation and k is the vertical translation. So, first we will graph the parent function of all cube root functions, p(x) = ³√x.

The graph of the parent function p(x) = ³√x is as follows:

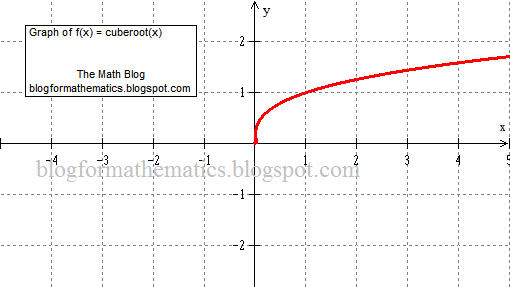Parent cube root function

Now in order to graph the function f(x) = ³√(x - 2) + 5, so you have to translate the graph of p(x) = ³√x two units right and five units up. Doing that, the graph of f(x) = ³√(x - 2) + 5 is obtained,

The above graph must look stretched horizontally and vertically, but it is only  translated right and up. In order to make the graph viewable, the axes has been taken such that the graph looks stretched.