Total number of combinations of n objects taken r at a time are calculated
by the formula
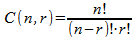 . Many other formulas related
to combinations can be derived from the above formula. These are termed as 'corollaries'. In total, we are going
to discuss five corollaries that can be derived from the above formula.
. Many other formulas related
to combinations can be derived from the above formula. These are termed as 'corollaries'. In total, we are going
to discuss five corollaries that can be derived from the above formula.
Corollary 1: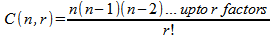
This corollary states that the combinations of n objects taken r at
a time are equal to the product of n, (n – 1), (n – 2),
.. up-to r factors divided by the factorial of r.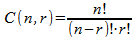 . Many other formulas related
to combinations can be derived from the above formula. These are termed as 'corollaries'. In total, we are going
to discuss five corollaries that can be derived from the above formula.
. Many other formulas related
to combinations can be derived from the above formula. These are termed as 'corollaries'. In total, we are going
to discuss five corollaries that can be derived from the above formula.Corollary 1:
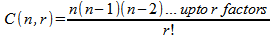
Proof:
Statement
|
Reason
|
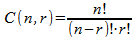 |
Formula for combinations |
 |
 |
 |
Canceling (n – r)! from)! from numerator and denominator |
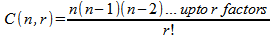 |
 |
Corollary 2:

This corollary states that there is only one possible combination when all
objects are taken at a time. That is, the combinations of objects taken n
at a time at a time are 1.
Proof:
Statement
|
Reason
Reason |
 |
Formula for combinations |
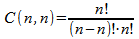 |
Substituting r = n because all objects are taken at a time. |
 |
()! equals (0)!, which is)!, which is equal to 1. |
 |
n! divided by n! equals 1. |
Corollary 3: or
or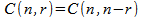
This corollary states that the number of combinations of n objects taken
r at a time is equal to the number of combinations of n objects taken
(n – r) at a time.
Proof:
Statement
|
Reason
|
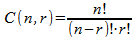 |
Formula for combinations |
 |
Substituting r = n – r |
 |
Simplifying the above formula |
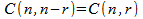 |
Comparing statements 1 and 3. |
Corollary 4:
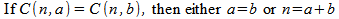
This corollary states that if the number of combinations of n objects taken
a at a time is equal to the number of combinations of n objects taken
b at a time, then either a and b are equal numbers, or the
the sum of a and b is equal to the total number of objects, n.
Proof:
Statement
|
Reason
|
 |
Given |
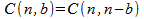 |
From Corollary 3 |
 |
From statements 1 and 2 |
 |
From above statement |
 |
From above statement |
Corollary 5:
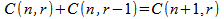 or
or
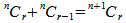
This corollary states that the sum of the number of combinations of n objects
taken r at a time and that of n objects taken r
– 1 at a time is equal to the number of combinations of n
+ 1 objects taken r at a time.Proof:
Statement
|
Reason
|
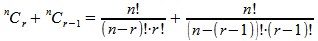 |
Applying the formula of combinations |
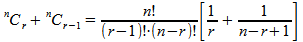 |
Simplifying the above statement by factoring |
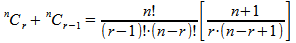 |
Adding the fractions |
| Simplifying the above statement | |
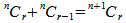 |
 |
No comments:
Post a Comment