The Quadratic Formula is derived by applying the method of completing the square on the standard form of a quadratic equation. Its complete derivation is given below:
General form of Quadratic Equation :

Divide throughout by 'a' (the coefficient of x-squared) :
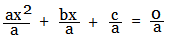
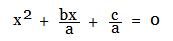
Move the term
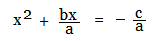
Take the coefficient of 'x', divide it by 2, then square it. Add the resulting term
to both sides of the quadratic equation :
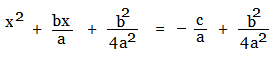
The LHS is now in the form of the expanded product of  because
because
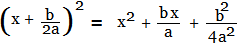
Thus rewriting it in its factored form,
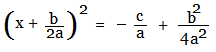 Simplifying the RHS,
Simplifying the RHS,
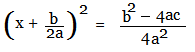 Taking square root of both sides,
Taking square root of both sides,
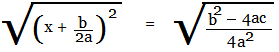 The square root of the LHS cancels out the exponent of 2 on it; The square root
The square root of the LHS cancels out the exponent of 2 on it; The square root
of '4a2' in the RHS is '2a', and the square root of the numerator of
the RHS is either positive or negative.
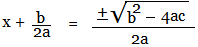
Move 'b/2a' to the RHS,
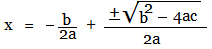
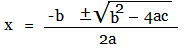 ,
,
which is the Quadratic Formula.
Thus the Quadratic Formula is derived from the standard form of a quadratic equation
by applying the method of completing the square on it.

to the RHS (Right Hand Side) :
to both sides of the quadratic equation :
Thus rewriting it in its factored form,
of '4a2' in the RHS is '2a', and the square root of the numerator of
the RHS is either positive or negative.
Move 'b/2a' to the RHS,
which is the Quadratic Formula.
by applying the method of completing the square on it.
No comments:
Post a Comment