 Example 1: x2 - 8x + 15 = 0
Example 1: x2 - 8x + 15 = 0Solution:
Step 1: Draw a box, divide it into
four equal boxes. Write the first term of the quadratic in box 1 and third term
in box 4.
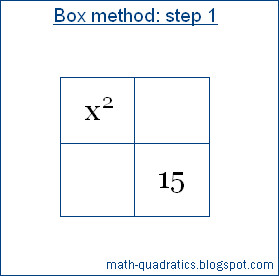
Step 2: Find two algebraic terms whose
product equals the product of box 1 and box 4, and whose sum equals the middle term
(or second term) of the quadratic. Write these two terms in boxes 2 and 3 respectively.

Step 3: Calculate the highest common
factor of each row and column and write it on the left of the row or at the top
of the column.

Step 4: The quadratic expression has
been factored. Take the two terms on the left of the rows and put a plus sign between
them. Similarly take the two terms at the top of the two columns and put a plus
sign between them. The product of these two algebraic expressions is equal to the
original quadratic expression.
x2 - 8x + 15 = (x - 3)(x - 5)
Step 5: Calculate the roots by applying
the Zero Product Rule
The quadratic equation obtained is: (x - 3)(x - 5) = 0. By applying the Zero Product
Rule, either (x - 3) is equal to zero, or (x - 5) is equal to zero.
Since (x - 3)(x - 5) = 0,
four equal boxes. Write the first term of the quadratic in box 1 and third term
in box 4.

Step 2: Find two algebraic terms whose
product equals the product of box 1 and box 4, and whose sum equals the middle term
(or second term) of the quadratic. Write these two terms in boxes 2 and 3 respectively.

Step 3: Calculate the highest common
factor of each row and column and write it on the left of the row or at the top
of the column.

Step 4: The quadratic expression has
been factored. Take the two terms on the left of the rows and put a plus sign between
them. Similarly take the two terms at the top of the two columns and put a plus
sign between them. The product of these two algebraic expressions is equal to the
original quadratic expression.
x2 - 8x + 15 = (x - 3)(x - 5)
Step 5: Calculate the roots by applying
the Zero Product Rule
The quadratic equation obtained is: (x - 3)(x - 5) = 0. By applying the Zero Product
Rule, either (x - 3) is equal to zero, or (x - 5) is equal to zero.
Since (x - 3)(x - 5) = 0,
- Either (x - 3) = 0, whence x = 3
- Or (x - 5) = 0, whence x = 5
Example 2: 16x = 4x2 + 15
Solution:
Solution:
First convert the given quadratic equation to the standard form:
four equal boxes. Write the first term of the quadratic in box 1 and third term
in box 4.

Step 2: Find two algebraic terms whose
product equals the product of box 1 and box 4, and whose sum equals the middle term
(or second term) of the quadratic. Write these two terms in boxes 2 and 3 respectively.

Step 3: Calculate the highest common
factor of each row and column and write it on the left of the row or at the top
of the column.

Step 4: The quadratic expression has
been factored. Take the two terms on the left of the rows and put a plus sign between
them. Similarly take the two terms at the top of the two columns and put a plus
sign between them. The product of these two algebraic expressions is equal to the
original quadratic expression.
4x2 - 16x + 15 = (2x - 3)(2x - 5)
Step 5: Calculate the roots by applying
the Zero Product Rule
The quadratic equation obtained is: (2x - 3)(2x - 5) = 0. By applying the Zero Product
Rule, either (2x - 3) is equal to zero, or (2x - 5) is equal to zero.
Since (2x - 3)(2x - 5) = 0, by applying the Zero Product Rule,
4x2 - 16x + 15 = 0
Step 1: Draw a box, divide it intofour equal boxes. Write the first term of the quadratic in box 1 and third term
in box 4.

Step 2: Find two algebraic terms whose
product equals the product of box 1 and box 4, and whose sum equals the middle term
(or second term) of the quadratic. Write these two terms in boxes 2 and 3 respectively.

Step 3: Calculate the highest common
factor of each row and column and write it on the left of the row or at the top
of the column.

Step 4: The quadratic expression has
been factored. Take the two terms on the left of the rows and put a plus sign between
them. Similarly take the two terms at the top of the two columns and put a plus
sign between them. The product of these two algebraic expressions is equal to the
original quadratic expression.
4x2 - 16x + 15 = (2x - 3)(2x - 5)
Step 5: Calculate the roots by applying
the Zero Product Rule
The quadratic equation obtained is: (2x - 3)(2x - 5) = 0. By applying the Zero Product
Rule, either (2x - 3) is equal to zero, or (2x - 5) is equal to zero.
Since (2x - 3)(2x - 5) = 0, by applying the Zero Product Rule,
- Either (2x - 3) = 0, whence x = 3/2
- Or (2x - 5) = 0, whence x = 5/2
Example 3: 3x2 + 5 = 8x
Solution:
Solution:
Convert the given quadratic equation to the standard form,
3x2 - 8x + 5 = 0
Step 1: Draw a box, divide it into
four equal boxes. Write the first term of the quadratic in box 1 and third term
in box 4.

Step 2: Find two algebraic terms whose
product equals the product of box 1 and box 4, and whose sum equals the middle term
(or second term) of the quadratic. Write these two terms in boxes 2 and 3 respectively.

Step 3: Calculate the highest common
factor of each row and column and write it on the left of the row or at the top
of the column.
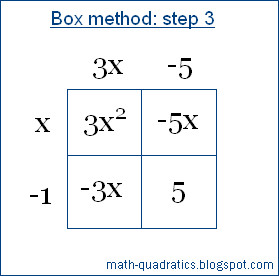
Step 4: The quadratic expression has
been factored. Take the two terms on the left of the rows and put a plus sign between
them. Similarly take the two terms at the top of the two columns and put a plus
sign between them. The product of these two algebraic expressions is equal to the
original quadratic expression.
3x2 - 8x + 5 = (x - 1)(3x - 5)
Step 5: Calculate the roots by applying
the Zero Product Rule
The quadratic equation obtained is: (x - 1)(3x - 5) = 0. By applying the Zero Product
Rule, either (x - 1) is equal to zero, or (3x - 5) is equal to zero.
Since (x - 1)(3x - 5) = 0, by applying Zero Product Rule,
3x2 - 8x + 5 = 0
Step 1: Draw a box, divide it into
four equal boxes. Write the first term of the quadratic in box 1 and third term
in box 4.

Step 2: Find two algebraic terms whose
product equals the product of box 1 and box 4, and whose sum equals the middle term
(or second term) of the quadratic. Write these two terms in boxes 2 and 3 respectively.

Step 3: Calculate the highest common
factor of each row and column and write it on the left of the row or at the top
of the column.

Step 4: The quadratic expression has
been factored. Take the two terms on the left of the rows and put a plus sign between
them. Similarly take the two terms at the top of the two columns and put a plus
sign between them. The product of these two algebraic expressions is equal to the
original quadratic expression.
3x2 - 8x + 5 = (x - 1)(3x - 5)
Step 5: Calculate the roots by applying
the Zero Product Rule
The quadratic equation obtained is: (x - 1)(3x - 5) = 0. By applying the Zero Product
Rule, either (x - 1) is equal to zero, or (3x - 5) is equal to zero.
Since (x - 1)(3x - 5) = 0, by applying Zero Product Rule,
- Either x - 1 = 0, whence x = 1
- Or 3x - 5 = 0, whence x = 5/3
Example 4: 2x2 + 5x = 12
Solution:
Solution:
Convert the given quadratic equation to the standard form,
four equal boxes. Write the first term of the quadratic in box 1 and third term
in box 4.
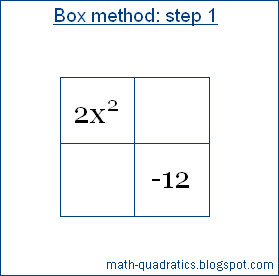
Step 2: Find two algebraic terms whose
product equals the product of box 1 and box 4, and whose sum equals the middle term
(or second term) of the quadratic. Write these two terms in boxes 2 and 3 respectively.

Step 3: Calculate the highest common
factor of each row and column and write it on the left of the row or at the top
of the column.

Step 4: The quadratic expression has
been factored. Take the two terms on the left of the rows and put a plus sign between
them. Similarly take the two terms at the top of the two columns and put a plus
sign between them. The product of these two algebraic expressions is equal to the
original quadratic expression.
2x2 + 5x - 12 = (x + 4)(2x - 3)
Step 5: Calculate the roots by applying
the Zero Product Rule
The quadratic equation obtained is: (x + 4)(2x - 3) = 0. By applying the Zero Product
Rule, either (x + 4) is equal to zero, or (2x - 3) is equal to zero.
Since (x + 4)(2x - 3) = 0, by applying the Zero Product Rule,
2x2 + 5x - 12 = 0
Step 1: Draw a box, divide it intofour equal boxes. Write the first term of the quadratic in box 1 and third term
in box 4.

Step 2: Find two algebraic terms whose
product equals the product of box 1 and box 4, and whose sum equals the middle term
(or second term) of the quadratic. Write these two terms in boxes 2 and 3 respectively.

Step 3: Calculate the highest common
factor of each row and column and write it on the left of the row or at the top
of the column.

Step 4: The quadratic expression has
been factored. Take the two terms on the left of the rows and put a plus sign between
them. Similarly take the two terms at the top of the two columns and put a plus
sign between them. The product of these two algebraic expressions is equal to the
original quadratic expression.
2x2 + 5x - 12 = (x + 4)(2x - 3)
Step 5: Calculate the roots by applying
the Zero Product Rule
The quadratic equation obtained is: (x + 4)(2x - 3) = 0. By applying the Zero Product
Rule, either (x + 4) is equal to zero, or (2x - 3) is equal to zero.
Since (x + 4)(2x - 3) = 0, by applying the Zero Product Rule,
- Either (x + 4) = 0, whence x = -4
- Or (2x - 3) = 0, whence x = 3/2
No comments:
Post a Comment